Fraction Calc

Fraction is a part of our daily lives. When we cook, eat, and drinks, there is always something that is less than a whole that we need to think of. Even on the environment around us, we experienced that fraction is always with us. Just imagine during half-moon and full moon, it signifies that even the nature has revealed its fraction form. But sometimes fraction can involve large numbers that is hard to comprehend, difficult to compute, and we may doubt that what we think that is right maybe wrong. In short, we need the fraction to be in its simplest form. The simpler, the better, and the easier to calculate. So to make a large fraction converted to its simplest form, we need the largest number that can divide both the numerator and denominator to make it through its lowest form. This number is what we called the greatest common factor or GCD.

The Other Methods

There are several methods to compute the greatest common factor.

• One is by listing all the factors for each number and selecting the largest factor that both numbers have in common. This is the most common method in finding the greatest common fraction but often left the student confused on how to list all the common factors.

  

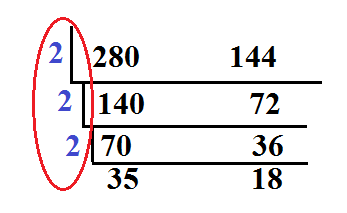
• The second method is called upside down division where both numbers are placed inside the upside down division bar and will be divided by a common factor. The process will be repeated using the result of the previous process until there is no more common factor that can process the result.

  

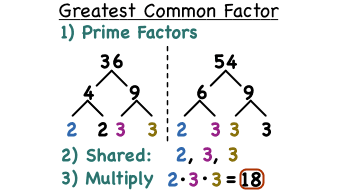
• The third is the prime factorization where the prime factors of each number are listed. Select all the prime factors that both numbers have in common and multiply those numbers by each other. The result is the greatest common factor.

  

• Then we have also a new method which is called Euclid's Algorithm.

What is Taught at School

I can never forget that listing all the factors of a certain number is very confusing for me at the beginning. It really takes a lot of mind power to get all those factors. Maybe this is the reason that many people don't like mathematics because one simple process might be a very tedious one. Listing all the factors is what my teacher taught me at that time. It took me a lot of practices to make my brain familiar of that method. Then in higher grades, my teacher introduced the prime factorization. This is a slight different because you have to list all the prime factors, get the common prime factors, and multiply by themselves. The product is now the GCM. Those are the two methods that were taught in school in my younger years.

The methods taught at school might be easy but requires a lot of energy. Listing the all the factors and prime factors may require a lot of thinking and burn enough energy. You may get tired easily at the beginning but with constant practice, you will gain mastery.

The Best Way

The most convenient way for me is by doing following steps:

1. Divide the bigger number by the smaller number and get the remainder.
2. If the remainder is lesser than the smaller number, the smaller number will now be the bigger number and the remainder will now be the smaller number. Otherwise, the remainder will be bigger number.
3. Repeat the process until the remainder is zero.
4. If the remainder is zero, smaller number the greatest common factor.

This method is very effective if it involves a large number but may not be a good idea if the numbers are smaller. That is why we have a mixed number calculator to make the computation easier.